Geometria delle Aree ~ formazione online

domenica 12 settembre 2010

Geometria delle Aree

Geometria delle Aree

Fissato un sistema di riferimento Cartesiano Oxy (per semplicità ortogonale, monometrico, destro), si definiscono:

Momento Statico

Momento d'Inerzia Assiale

Il significato dimenticato

A volte alcuni concetti matematici vengono studiati e poi ripetutamente applicati per la risoluzione di importanti problemi tecnici. Il concetto di baricentro per esempio, è essenziale nel calcolo di progetto di una trave di un ponte, tuttavia ciò facendo si può perdere la consapevolezza del significato fisico originario di baricentro ovvero di momento statico.
Calcoliamo il momento statico di una figura scomponendola in figure elementari per ottenerne il centro di massa complessivo, senza chiederci cosa sia. In questo post vogliamo porre rimedio a questa potenziale lacuna…

Definizione geometrica di momento statico

Il momento statico o momento del primo ordine di una figura dal dominio V, con riferimento ad un piano $\gamma$ , è l’integrale:

$\displaystyle S_\gamma=\int_V h_\gamma \, dV.$

dove $h_\gamma$ è la distanza ortogonale con segno del punto della figura dal piano $\gamma$ . In sostanza si tratta del prodotto di un volume per la sua distanza dal piano di riferimento.

Momento statico e sistema di masse puntiformi

Per un sistema di masse puntiformi $m_1, m_2, \dots, m_k$ il momento statico rispetto ad un piano $\gamma$ è la somma dei prodotti delle masse per la rispettiva distanza $h_i$ dal piano considerato. In formule:

$\displaystyle S_\gamma = \sum_i^k m_i h_i.$

Dividendo il momento statico per la massa totale del sistema si ottiene la distanza del baricentro da quel piano $\gamma$ , quindi se si considerano tre piani a due a due non paralleli si determina la posizione del baricentro del sistema di masse dalla loro intersezione.

Sistemi equivalenti

Due sistemi vettoriali sono equivalenti se hanno la stessa somma (risultante) e se rispetto ad un polo, hanno lo stesso momento.
Per capire quale sia il significato fisico del momento statico, introduciamo un sistema di vettori paralleli $\boldsymbol{v_i}$ applicati nei punti $P_i$ , e ricerchiamone un secondo sistema equivalente composto da un unico vettore. Indichiamo anche con $\boldsymbol{u}$ il versore relativo alla direzione dei vettori, quindi tale che $\boldsymbol{v_i}= m_i \boldsymbol{u}$ , dove lo scalare $m_i$ è appunto la componente vettoriale.
La risultante, somma dei vettori $\boldsymbol{v_i}$ è il vettore $\boldsymbol{V}$ che si scrive:

$\boldsymbol{V} = \sum_i \boldsymbol{v_i} = (\sum_i m_i)\boldsymbol{u} = m \boldsymbol{u}$ .

La risultante sarà un sitema equivalente al primo se il momento rispetto ad un punto sarà lo stesso. Per saperne di più sul prodotto vettoriale consultare la
Il momento del sistema di vettori paralleli è la somma dei vettori prodotto tra il vettore $\boldsymbol{OP_i}$ ed il vettore $\boldsymbol{v_i}$ :

$\displaystyle \boldsymbol{M} = \sum_i \boldsymbol{OP_i} \times \boldsymbol{v_i} = \sum_i m_i \boldsymbol{OP_i} \times \boldsymbol{u}.$ .

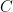
Il momento rispetto allo stesso polo della risultante $\boldsymbol{V}$ , indicando con $C$ il punto di applicazione della risultante, è:

$\displaystyle \boldsymbol{M}=\boldsymbol{OC} \times \boldsymbol{V} = m \boldsymbol{OC} \times \boldsymbol{u}.$

L’uguaglianza dei due momenti impone l’uguaglianza dei vettori primi termini del prodotto così che otteniamo la relazione:

$\displaystyle m \boldsymbol{OC} = \sum_i m_i \boldsymbol{OP_i}.$

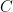
Da quì è possibile trovare il punto di applicazione $C$ , detto centro dei vettori, della risultante $\boldsymbol{V}$ , riscrivendo la precedente relazione vettoriale per ciascuna componente relativa ad una terna cartesiana $O, x, y, z$ di riferimento, se facciamo coincidere il polo $O$ con l’origine otteniamo:

$\displaystyle m \, x_c = \sum_i m_i x_i,$

$\displaystyle m \, y_c = \sum_i m_i y_i,$

$\displaystyle m \, z_c = \sum_i m_i z_i.$

I secondi membri delle equazioni scritte sopra sono i momenti statici rispetto ai piani coordinati di un sistema puntiforme $m_i$ , corrispondenti alle componenti del momento risultante del sistema stesso.

I momenti statici discendono quindi dal principio di equivalenza di un sistema di vettori paralleli con un unico vettore risultante.

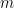
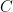
Da qui il passo per giungere al baricentro è semplice. Basta introdurre un campo gravitazionale omogeneo e considerare quale sistema di vettori paralleli le forze peso. In questo caso le componenti $m_i$ hanno valore solo positivo essendo le singole masse (a meno di non considerare corpi di antimateria!), $m$ sarà la massa complessiva ed il centro $C$ diventerà il baricentro $G$ .
Le forze peso sono infatti $m_i g$ dove $g$ è l’accelerazione gravitazionale che è costante pertanto nelle relazioni scompare e rimane solo la massa.
Per i sistemi continui occorre introdurre il calcolo integrale considerando il valore della massa in funzione della densità $\delta$ ovvero scrivendo in differenziali $dm = \delta \, dV$ . I momenti statici si scriveranno come integrali di $x dm = x \delta dV$ . Ulteriore classica semplificazione è assumere la densità costante, e scrivere in definitiva le coordinate del baricentro di un corpo di volume V:

$\displaystyle V x_G = \int_V x \, dV,$